<transform-function>
Baseline Widely available
This feature is well established and works across many devices and browser versions. It’s been available across browsers since September 2015.
Der <transform-function> CSS Datentyp repräsentiert eine Transformation, die das Erscheinungsbild eines Elements beeinflusst. Transformationsfunktionen können ein Element in 2D- oder 3D-Raum drehen, skalieren, verzerren oder verschieben. Dieser Datentyp wird in der transform-Eigenschaft verwendet.
Syntax
Der <transform-function>-Datentyp wird mithilfe einer der unten aufgeführten Transformationsfunktionen angegeben. Jede Funktion führt eine geometrische Operation entweder in 2D oder 3D durch.
Matrixtransformation
matrix()-
Beschreibt eine homogene 2D-Transformationsmatrix.
matrix3d()-
Beschreibt eine 3D-Transformation als 4×4-homogene Matrix.
Perspektive
perspective()-
Legt den Abstand zwischen dem Benutzer und der z=0-Ebene fest.
Rotation
rotate()-
Dreht ein Element um einen festen Punkt auf der 2D-Ebene.
rotate3d()-
Dreht ein Element um eine feste Achse im 3D-Raum.
rotateX()-
Dreht ein Element um die horizontale Achse.
rotateY()-
Dreht ein Element um die vertikale Achse.
rotateZ()-
Dreht ein Element um die z-Achse.
Skalierung (Größenänderung)
scale()-
Vergrößert oder verkleinert ein Element auf der 2D-Ebene.
scale3d()-
Vergrößert oder verkleinert ein Element im 3D-Raum.
scaleX()-
Vergrößert oder verkleinert ein Element horizontal.
scaleY()-
Vergrößert oder verkleinert ein Element vertikal.
scaleZ()-
Vergrößert oder verkleinert ein Element entlang der z-Achse.
Verzerrung (Schrägstellung)
Translation (Verschiebung)
translate()-
Verschiebt ein Element auf der 2D-Ebene.
translate3d()-
Verschiebt ein Element im 3D-Raum.
translateX()-
Verschiebt ein Element horizontal.
translateY()-
Verschiebt ein Element vertikal.
translateZ()-
Verschiebt ein Element entlang der z-Achse.
Beschreibung
Verschiedene Koordinatenmodelle können verwendet werden, um die Größe und Form eines HTML-Elements sowie jede darauf angewendete Transformation zu beschreiben. Am häufigsten wird das kartesische Koordinatensystem verwendet, obwohl auch homogene Koordinaten manchmal zum Einsatz kommen.
Kartesische Koordinaten
Im kartesischen Koordinatensystem wird ein zweidimensionaler Punkt mit zwei Werten beschrieben: einer x-Koordinate (Abszisse) und einer y-Koordinate (Ordinate). Dies wird durch die Vektorschreibweise (x, y) dargestellt.
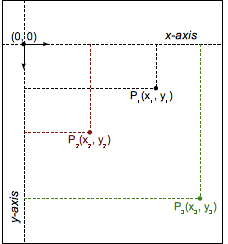
In CSS (und den meisten Grafiksystemen) steht der Ursprung (0, 0) für die linke obere Ecke eines Elements. Positive Koordinaten liegen unterhalb und rechts vom Ursprung, während negative oberhalb und links davon liegen. Ein Punkt 2 Einheiten nach rechts und 5 Einheiten nach unten würde also (2, 5) sein, während ein Punkt 3 Einheiten nach links und 12 Einheiten nach oben (-3, -12) wäre.
Transformationsfunktionen
Transformationsfunktionen verändern das Erscheinungsbild eines Elements, indem sie die Werte seiner Koordinaten manipulieren. Eine lineare Transformationsfunktion wird durch eine 2×2-Matrix beschrieben, wie folgt:
Die Funktion wird durch Matrixmultiplikation auf ein Element angewendet, wodurch sich jede Koordinate basierend auf den Werten in der Matrix ändert:
Es ist sogar möglich, mehrere Transformationen hintereinander anzuwenden:
Mit dieser Notation lässt sich die Mehrzahl der üblichen Transformationen – Rotationen, Skalierungen oder Schrägstellungen – beschreiben und zusammensetzen. (Tatsächlich können alle Transformationen beschrieben werden, die lineare Funktionen darstellen.) Zusammengesetzte Transformationen werden effektiv von rechts nach links angewendet.
Allerdings gibt es eine wichtige Transformation, die nicht linear ist und daher in dieser Notation gesondert berücksichtigt werden muss: die Translation. Der Translationsvektor (tx, ty) muss separat als zwei zusätzliche Parameter beschrieben werden.
Hinweis: Obwohl sie schwieriger als kartesische Koordinaten sind, führen homogene Koordinaten in der projektiven Geometrie zu 3×3-Transformationsmatrizen und können Übersetzungen als lineare Funktionen ausdrücken.
Beispiele
Vergleich von Transformationsfunktionen
Das folgende Beispiel zeigt einen 3D-Würfel, der aus DOM-Elementen und Transformationen erstellt wurde, sowie ein Auswahlmenü, mit dem Sie verschiedene Transformationsfunktionen auswählen können, um den Würfel zu transformieren und die Auswirkungen der verschiedenen Typen zu vergleichen.
Wählen Sie eine Option, und die Transformation wird auf den Würfel angewendet; nach 2 Sekunden kehrt der Würfel zu seinem Ausgangszustand zurück. Der Ausgangszustand des Würfels ist mit transform3d() leicht gedreht, um die Wirkung aller Transformationen sichtbarer zu machen.
HTML
<main>
<section id="example-element">
<div class="face front">1</div>
<div class="face back">2</div>
<div class="face right">3</div>
<div class="face left">4</div>
<div class="face top">5</div>
<div class="face bottom">6</div>
</section>
<div class="select-form">
<label for="transfunction">Select a transform function</label>
<select id="transfunction">
<option selected>Choose a function</option>
<option>rotate(360deg)</option>
<option>rotateX(360deg)</option>
<option>rotateY(360deg)</option>
<option>rotateZ(360deg)</option>
<option>rotate3d(1, 1, 1, 90deg)</option>
<option>scale(1.5)</option>
<option>scaleX(1.5)</option>
<option>scaleY(1.5)</option>
<option>scaleZ(1.5)</option>
<option>scale3d(1, 1.5, 1.5)</option>
<option>skew(17deg, 13deg)</option>
<option>skewX(17deg)</option>
<option>skewY(17deg)</option>
<option>translate(100px, 100px)</option>
<option>translateX(100px)</option>
<option>translateY(100px)</option>
<option>translateZ(100px)</option>
<option>translate3d(50px, 50px, 50px)</option>
<option>perspective(200px)</option>
<option>matrix(1, 2, -1, 1, 80, 80)</option>
<option>matrix3d(1,0,0,0,0,1,3,0,0,0,1,0,50,100,0,1.1)</option>
</select>
</div>
</main>
CSS
main {
width: 400px;
height: 200px;
padding: 50px;
background-image: linear-gradient(135deg, white, cyan, white);
}
#example-element {
width: 100px;
height: 100px;
transform-style: preserve-3d;
transition: transform 1.5s;
transform: rotate3d(1, 1, 1, 30deg);
}
.face {
display: flex;
align-items: center;
justify-content: center;
width: 100%;
height: 100%;
position: absolute;
backface-visibility: inherit;
font-size: 60px;
color: #fff;
}
.front {
background: rgb(90 90 90 / 70%);
transform: translateZ(50px);
}
.back {
background: rgb(0 210 0 / 70%);
transform: rotateY(180deg) translateZ(50px);
}
.right {
background: rgb(210 0 0 / 70%);
transform: rotateY(90deg) translateZ(50px);
}
.left {
background: rgb(0 0 210 / 70%);
transform: rotateY(-90deg) translateZ(50px);
}
.top {
background: rgb(210 210 0 / 70%);
transform: rotateX(90deg) translateZ(50px);
}
.bottom {
background: rgb(210 0 210 / 70%);
transform: rotateX(-90deg) translateZ(50px);
}
.select-form {
margin-top: 50px;
}
JavaScript
const selectElem = document.querySelector("select");
const example = document.querySelector("#example-element");
selectElem.addEventListener("change", () => {
if (selectElem.value === "Choose a function") {
return;
} else {
example.style.transform = `rotate3d(1, 1, 1, 30deg) ${selectElem.value}`;
setTimeout(() => {
example.style.transform = "rotate3d(1, 1, 1, 30deg)";
}, 2000);
}
});
Ergebnis
Spezifikationen
| Specification |
|---|
| CSS Transforms Module Level 1 # transform-functions |
| CSS Transforms Module Level 2 # transform-functions |
Browser-Kompatibilität
BCD tables only load in the browser