WebGL-Modellansicht-Projektion
Dieser Artikel untersucht, wie Daten in einem WebGL-Projekt projiziert werden, um sie auf dem Bildschirm anzuzeigen. Es wird vorausgesetzt, dass Sie grundlegende Kenntnisse in Matrizenmathematik mit Übersetzungs-, Skalierungs- und Rotationsmatrizen haben. Er erklärt die drei Kernmatrizen, die typischerweise beim Erstellen einer 3D-Szene verwendet werden: die Modell-, Betrachtungs- und Projektionsmatrizen.
Hinweis:
Dieser Artikel ist auch als MDN-Inhalts-Kit verfügbar. Es wird auch eine Sammlung von Hilfsfunktionen verwendet, die unter dem globalen Objekt MDN verfügbar sind.
Die Modell-, Betrachtungs- und Projektionsmatrizen
Individuelle Transformationen von Punkten und Polygonen im Raum werden in WebGL von den grundlegenden Transformationsmatrizen wie Übersetzung, Skalierung und Rotation gehandhabt. Diese Matrizen können zusammengesetzt und auf besondere Weise gruppiert werden, um sie für das Rendern komplizierter 3D-Szenen nützlich zu machen. Diese zusammengesetzten Matrizen bewegen die ursprünglichen Modelldaten letztendlich in einen speziellen Koordinatenraum, der als Clip Space bezeichnet wird. Dies ist ein 2 Einheiten breiter Würfel, zentriert bei (0,0,0), mit Ecken, die von (-1,-1,-1) bis (1,1,1) reichen. Dieser Clip Space wird in einen 2D-Raum komprimiert und in ein Bild rasterisiert.
Die erste hier besprochene Matrix ist die Modellmatrix, die definiert, wie Sie Ihre ursprünglichen Modelldaten im 3D-Weltraum bewegen. Die Projektionsmatrix wird verwendet, um Weltkoordinaten in Clip-Space-Koordinaten zu konvertieren. Eine häufig verwendete Projektionsmatrix, die Perspektivprojektionsmatrix, wird verwendet, um die Effekte einer typischen Kamera zu imitieren, die als Vertreter für den Betrachter in der 3D-Virtualwelt dient. Die Betrachtungsmatrix ist verantwortlich dafür, die Objekte in der Szene zu bewegen, um die Änderung der Kameraposition zu simulieren, und verändert, was der Betrachter aktuell sehen kann.
Die folgenden Abschnitte bieten einen tiefen Einblick in die Ideen hinter und die Implementierung der Modell-, Betrachtungs- und Projektionsmatrizen. Diese Matrizen sind zentral, um Daten auf dem Bildschirm zu bewegen, und sie sind Konzepte, die individuelle Frameworks und Engines überschreiten.
Clip Space
In einem WebGL-Programm werden Daten typischerweise mit einem eigenen Koordinatensystem an die GPU hochgeladen, und der Vertex-Shader transformiert diese Punkte in ein spezielles Koordinatensystem, das als Clip Space bekannt ist. Alle Daten, die sich außerhalb des Clip Space befinden, werden abgeschnitten und nicht gerendert. Wenn jedoch ein Dreieck die Grenze dieses Raums überschreitet, wird es in neue Dreiecke zerteilt, und nur die Teile der neuen Dreiecke, die im Clip Space liegen, werden behalten.
Die obige Grafik ist eine Visualisierung des Clip Space, in den alle Punkte passen müssen. Es ist ein Würfel mit zwei Einheiten auf jeder Seite, wobei eine Ecke bei (-1,-1,-1) und die gegenüberliegende Ecke bei (1,1,1) liegt. Die Mitte des Würfels ist der Punkt (0,0,0). Dieses 8-Kubikmeter-Koordinatensystem, das vom Clip Space verwendet wird, ist als normalisierte Gerätekoordinaten (NDC) bekannt. Ihnen könnte dieser Begriff begegnen, während Sie sich informieren und mit WebGL-Code arbeiten.
Für diesen Abschnitt werden wir unsere Daten direkt in das Koordinatensystem des Clip Space einbringen. Normalerweise verwendet man Modelldaten, die sich in einem beliebigen Koordinatensystem befinden, und transformiert diese dann mithilfe einer Matrix, um die Modellkoordinaten in das Koordinatensystem des Clip Space zu konvertieren. Für dieses Beispiel ist es am einfachsten, zu veranschaulichen, wie der Clip Space funktioniert, indem wir Modellkoordinatenwerte von (-1,-1,-1) bis (1,1,1) verwenden. Der folgende Code wird 2 Dreiecke erstellen, die ein Quadrat auf dem Bildschirm zeichnen. Die Z-Tiefe in den Quadraten bestimmt, was oben gezeichnet wird, wenn die Quadrate den gleichen Raum teilen. Die kleineren Z-Werte werden über den größeren Z-Werten gerendert.
WebGLBox-Beispiel
Dieses Beispiel wird ein benutzerdefiniertes WebGLBox-Objekt erstellen, das ein 2D-Quadrat auf dem Bildschirm zeichnet.
Hinweis: Der Code für jedes WebGLBox-Beispiel ist in diesem GitHub-Repo verfügbar und nach Abschnitt organisiert. Darüber hinaus gibt es unten in jedem Abschnitt einen JSFiddle-Link.
WebGLBox-Konstruktor
Der Konstruktor sieht so aus:
function WebGLBox() {
// Setup the canvas and WebGL context
this.canvas = document.getElementById("canvas");
this.canvas.width = window.innerWidth;
this.canvas.height = window.innerHeight;
this.gl = MDN.createContext(canvas);
const gl = this.gl;
// Setup a WebGL program, anything part of the MDN object is defined outside of this article
this.webglProgram = MDN.createWebGLProgramFromIds(
gl,
"vertex-shader",
"fragment-shader",
);
gl.useProgram(this.webglProgram);
// Save the attribute and uniform locations
this.positionLocation = gl.getAttribLocation(this.webglProgram, "position");
this.colorLocation = gl.getUniformLocation(this.webglProgram, "color");
// Tell WebGL to test the depth when drawing, so if a square is behind
// another square it won't be drawn
gl.enable(gl.DEPTH_TEST);
}
WebGLBox-Zeichnen
Jetzt erstellen wir eine Methode, um ein Quadrat auf dem Bildschirm zu zeichnen.
WebGLBox.prototype.draw = function (settings) {
// Create some attribute data; these are the triangles that will end being
// drawn to the screen. There are two that form a square.
const data = new Float32Array([
//Triangle 1
settings.left,
settings.bottom,
settings.depth,
settings.right,
settings.bottom,
settings.depth,
settings.left,
settings.top,
settings.depth,
//Triangle 2
settings.left,
settings.top,
settings.depth,
settings.right,
settings.bottom,
settings.depth,
settings.right,
settings.top,
settings.depth,
]);
// Use WebGL to draw this onto the screen.
// Performance Note: Creating a new array buffer for every draw call is slow.
// This function is for illustration purposes only.
const gl = this.gl;
// Create a buffer and bind the data
const buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
// Setup the pointer to our attribute data (the triangles)
gl.enableVertexAttribArray(this.positionLocation);
gl.vertexAttribPointer(this.positionLocation, 3, gl.FLOAT, false, 0, 0);
// Setup the color uniform that will be shared across all triangles
gl.uniform4fv(this.colorLocation, settings.color);
// Draw the triangles to the screen
gl.drawArrays(gl.TRIANGLES, 0, 6);
};
Die Shader sind die Codebits, die in GLSL geschrieben sind und unsere Datenpunkte letztendlich auf dem Bildschirm rendern. Diese Shader werden aus Bequemlichkeit in einem <script>-Element gespeichert, das über die benutzerdefinierte Funktion MDN.createWebGLProgramFromIds() in das Programm eingebracht wird. Diese Funktion ist Teil einer Sammlung von Hilfsfunktionen, die für diese Tutorials geschrieben wurden und hier nicht ausführlich erklärt werden. Diese Funktion übernimmt die Grundlagen der Umwandlung von GLSL-Quellcode in ein WebGL-Programm. Die Funktion nimmt drei Parameter - den Kontext, in dem das Programm gerendert werden soll, die ID des <script>-Elements für den Vertex-Shader und die ID des <script>-Elements für den Fragment-Shader. Der Vertex-Shader positioniert die Vertizes, und der Fragment-Shader färbt jedes Pixel.
Schauen Sie sich zuerst den Vertex-Shader an, der die Vertices auf dem Bildschirm bewegen wird:
// The individual position vertex
attribute vec3 position;
void main() {
// the gl_Position is the final position in clip space after the vertex shader modifies it
gl_Position = vec4(position, 1.0);
}
Als nächstes, um die Daten tatsächlich in Pixel zu rasterisieren, bewertet der Fragment-Shader alles auf einer Pixel-zu-Pixel-Basis und setzt eine einzige Farbe. Die GPU ruft die Shader-Funktion für jedes Pixel, das sie rendern muss, auf; die Aufgabe des Shaders besteht darin, die Farbe für dieses Pixel zurückzugeben.
precision mediump float;
uniform vec4 color;
void main() {
gl_FragColor = color;
}
Mit diesen Einstellungen ist es Zeit, direkt mit Clip-Space-Koordinaten auf den Bildschirm zu zeichnen.
const box = new WebGLBox();
Zuerst ein rotes Quadrat in die Mitte zeichnen.
box.draw({
top: 0.5, // x
bottom: -0.5, // x
left: -0.5, // y
right: 0.5, // y
depth: 0, // z
color: [1, 0.4, 0.4, 1], // red
});
Als nächstes ein grünes Quadrat oben und hinter dem roten Quadrat zeichnen.
box.draw({
top: 0.9, // x
bottom: 0, // x
left: -0.9, // y
right: 0.9, // y
depth: 0.5, // z
color: [0.4, 1, 0.4, 1], // green
});
Schließlich, um zu demonstrieren, dass Clipping tatsächlich stattfindet, wird dieses Quadrat nicht gezeichnet, da es vollständig außerhalb des Clip Space ist. Die Tiefe liegt außerhalb des Bereichs von -1.0 bis 1.0.
box.draw({
top: 1, // x
bottom: -1, // x
left: -1, // y
right: 1, // y
depth: -1.5, // z
color: [0.4, 0.4, 1, 1], // blue
});
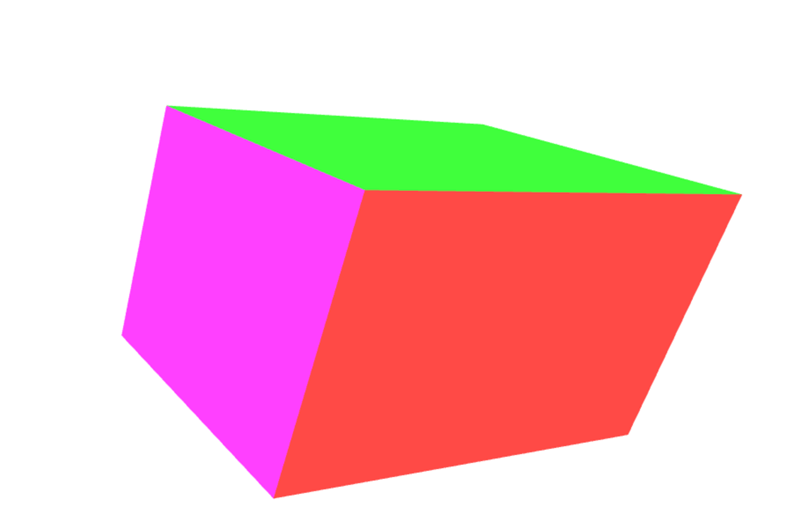
Die Ergebnisse
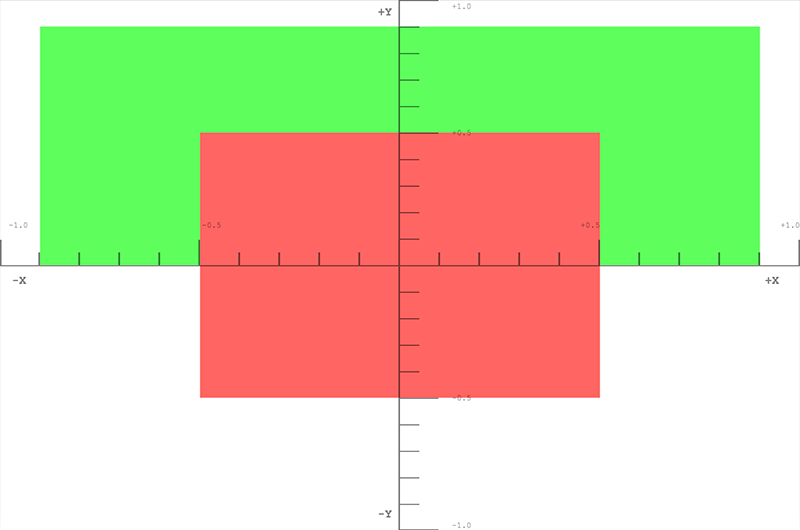
Übung
Eine hilfreiche Übung an dieser Stelle ist, die Quadrate im Clip Space zu bewegen, indem der Code variiert wird, um ein Gefühl dafür zu bekommen, wie Punkte im Clip Space abgeschnitten und bewegt werden. Versuchen Sie, ein Bild wie ein kastiges Smiley-Gesicht mit einem Hintergrund zu zeichnen.
Homogene Koordinaten
Die Hauptlinie des vorherigen Clip-Spaces-Vertex-Shaders enthielt diesen Code:
gl_Position = vec4(position, 1.0);
Die Variable position wurde in der Methode draw() definiert und als Attribut an den Shader übergeben. Dies ist ein dreidimensionaler Punkt, aber die Variable gl_Position, die durch den Pipeline-Prozess weitergegeben wird, ist tatsächlich 4-dimensional — anstelle von (x, y, z) ist es (x, y, z, w). Es gibt keinen Buchstaben nach z, daher wird diese vierte Dimension konventionell als w bezeichnet. Im obigen Beispiel ist die w-Koordinate auf 1.0 gesetzt.
Die naheliegende Frage ist "warum die zusätzliche Dimension?" Es stellt sich heraus, dass diese Ergänzung viele schöne Techniken zur Manipulation von 3D-Daten ermöglicht. Diese hinzugefügte Dimension führt die Vorstellung von Perspektive in das Koordinatensystem ein; damit können wir 3D-Koordinaten in den 2D-Raum abbilden — wodurch es ermöglicht wird, dass zwei parallele Linien als sie als sie in die Ferne rücken, sich schneiden. Der Wert von w wird als Divisor für die anderen Komponenten der Koordinate verwendet, so dass die tatsächlichen Werte von x, y und z als x/w, y/w und z/w berechnet werden (und w ist dann auch w/w und wird zu 1).
Ein dreidimensionaler Punkt ist in einem typischen kartesischen Koordinatensystem definiert. Die hinzugefügte vierte Dimension verwandelt diesen Punkt in eine homogene Koordinate. Es stellt immer noch einen Punkt im 3D-Raum dar und es kann leicht demonstriert werden, wie man diese Art von Koordinate durch ein Paar einfacher Funktionen konstruieren kann.
function cartesianToHomogeneous(point) {
let x = point[0];
let y = point[1];
let z = point[2];
return [x, y, z, 1];
}
function homogeneousToCartesian(point) {
let x = point[0];
let y = point[1];
let z = point[2];
let w = point[3];
return [x / w, y / w, z / w];
}
Wie bereits erwähnt und in den obigen Funktionen gezeigt, teilt die w-Komponente die x-, y- und z-Komponenten. Wenn die w-Komponente eine von Null verschiedene reelle Zahl ist, kann die homogene Koordinate leicht in einen normalen Punkt im kartesischen Raum übersetzt werden. Was passiert nun, wenn die w-Komponente Null ist? In JavaScript würde der zurückgegebene Wert wie folgt aussehen.
homogeneousToCartesian([10, 4, 5, 0]);
Dies ergibt: [Infinity, Infinity, Infinity].
Diese homogene Koordinate stellt irgendeinen Punkt im Unendlichen dar. Dies ist eine praktische Möglichkeit, einen Strahl zu repräsentieren, der vom Ursprung in eine bestimmte Richtung schießt. Neben einem Strahl könnte es auch als Darstellung eines Richtungsvektors angesehen werden. Wenn diese homogene Koordinate mit einer Matrix mit einer Übersetzung multipliziert wird, wird die Übersetzung effektiv herausgefiltert.
Wenn Zahlen auf Computern extrem groß (oder extrem klein) sind, werden sie immer ungenauer, weil sie nur mit so vielen Einsen und Nullen repräsentiert werden können. Je mehr Operationen auf größeren Zahlen durchgeführt werden, desto mehr Fehler sammeln sich im Ergebnis an. Wenn durch w geteilt wird, kann dies effektiv die Genauigkeit sehr großer Zahlen erhöhen, indem auf zwei potenziell kleinere, weniger fehleranfällige Zahlen gearbeitet wird.
Der letzte Vorteil der Verwendung homogener Koordinaten ist, dass sie sehr gut für die Multiplikation mit 4x4 Matrizen geeignet sind. Ein Vertex muss mindestens eine der Dimensionen einer Matrix erfüllen, um mit ihr multipliziert zu werden. Die 4x4-Matrix kann verwendet werden, um eine Vielzahl von nützlichen Transformationen zu kodieren. Tatsächlich nutzt die typische Perspektivprojektionsmatrix die Division durch die w-Komponente, um ihre Transformation durchzuführen.
Das Abschneiden von Punkten und Polygonen aus dem Clip Space erfolgt, bevor die homogenen Koordinaten zurück in kartesische Koordinaten transformiert wurden (durch Division durch w). Dieser finale Raum wird als normalisierte Gerätekoordinaten oder NDC bezeichnet.
Um mit dieser Idee zu spielen, kann das vorherige Beispiel modifiziert werden, um die Verwendung der w-Komponente zu ermöglichen.
//Redefine the triangles to use the W component
const data = new Float32Array([
//Triangle 1
settings.left,
settings.bottom,
settings.depth,
settings.w,
settings.right,
settings.bottom,
settings.depth,
settings.w,
settings.left,
settings.top,
settings.depth,
settings.w,
//Triangle 2
settings.left,
settings.top,
settings.depth,
settings.w,
settings.right,
settings.bottom,
settings.depth,
settings.w,
settings.right,
settings.top,
settings.depth,
settings.w,
]);
Dann verwendet der Vertex-Shader den übergebenen 4-dimensionalen Punkt.
attribute vec4 position;
void main() {
gl_Position = position;
}
Zuerst zeichnen wir ein rotes Quadrat in die Mitte, setzen aber W auf 0.7. Da die Koordinaten durch 0.7 geteilt werden, werden sie alle vergrößert.
box.draw({
top: 0.5, // y
bottom: -0.5, // y
left: -0.5, // x
right: 0.5, // x
w: 0.7, // w - enlarge this box
depth: 0, // z
color: [1, 0.4, 0.4, 1], // red
});
Jetzt zeichnen wir ein grünes Quadrat oben, verkleinern es aber, indem wir die w-Komponente auf 1.1 setzen.
box.draw({
top: 0.9, // y
bottom: 0, // y
left: -0.9, // x
right: 0.9, // x
w: 1.1, // w - shrink this box
depth: 0.5, // z
color: [0.4, 1, 0.4, 1], // green
});
Dieses letzte Quadrat wird nicht gezeichnet, weil es außerhalb des Clip Space liegt. Die Tiefe liegt außerhalb des Bereichs von -1.0 bis 1.0.
box.draw({
top: 1, // y
bottom: -1, // y
left: -1, // x
right: 1, // x
w: 1.5, // w - Bring this box into range
depth: -1.5, // z
color: [0.4, 0.4, 1, 1], // blue
});
Die Ergebnisse
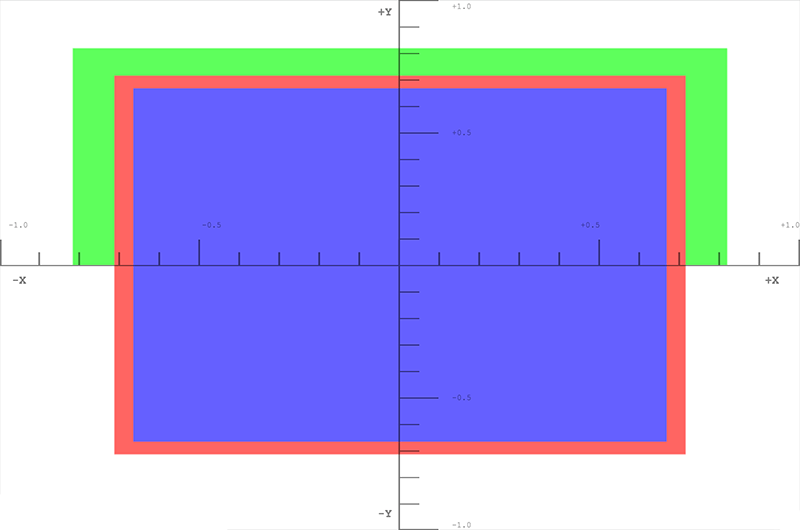
Übungen
- Spielen Sie mit diesen Werten, um zu sehen, wie sie das, was auf dem Bildschirm gerendert wird, beeinflussen. Beachten Sie, wie das zuvor abgeschnittene blaue Quadrat zurück in den Bereich gebracht wird, indem seine
w-Komponente gesetzt wird. - Versuchen Sie, ein neues Quadrat zu erstellen, das außerhalb des Clip Space liegt, und bringen Sie es zurück, indem Sie durch
wteilen.
Modelltransformation
Punkte direkt in den Clip Space zu setzen ist von begrenztem Nutzen. In realen Anwendungen liegen Ihre Quellkoordinaten nicht bereits in Clip Space-Koordinaten vor. In den meisten Fällen müssen Sie die Modell- und andere Koordinaten in den Clip Space transformieren. Der bescheidene Würfel ist ein einfaches Beispiel dafür, wie dies zu tun ist. Die Würfeldaten bestehen aus den Scheitelpunktpositionen, den Farben der Würfelseiten und der Reihenfolge der Scheitelpunktpositionen, die die einzelnen Polygone bilden (in Gruppen von 3 Scheitelpunkten, um die Dreiecke zu konstruieren, die die Würfelseiten bilden). Die Positionen und Farben werden in GL-Puffern gespeichert, als Attribute an den Shader gesendet und dann individuell darauf operiert.
Schließlich wird eine einzelne Modellmatrix berechnet und gesetzt. Diese Matrix repräsentiert die Transformationen, die an jedem Punkt vorgenommen werden müssen, der das Modell ausmacht, um es in den richtigen Raum zu bewegen und alle anderen erforderlichen Transformationen für jeden Punkt im Modell durchzuführen. Dies gilt nicht nur für jeden Scheitelpunkt, sondern auch für jeden Punkt auf jeder Fläche des Modells.
In diesem Fall wird für jedes Bild der Animation eine Reihe von Skalierungs-, Rotations- und Übersetzungsmatrizen verwendet, um die Daten in die gewünschte Position im Clip Space zu bringen. Der Würfel hat die Größe des Clip Space (-1,-1,-1) bis (1,1,1), also muss er verkleinert werden, um nicht den gesamten Clip Space auszufüllen. Diese Matrix wird direkt an den Shader gesendet, nachdem sie zuvor in JavaScript multipliziert wurde.
Der folgende Codeausschnitt definiert eine Methode im CubeDemo-Objekt, die die Modellmatrix erstellen wird. Er verwendet benutzerdefinierte Funktionen zur Erstellung und Multiplikation von Matrizen, wie sie im MDN WebGL-Shared Code definiert sind. Die neue Funktion sieht folgendermaßen aus:
CubeDemo.prototype.computeModelMatrix = function (now) {
//Scale down by 50%
const scale = MDN.scaleMatrix(0.5, 0.5, 0.5);
// Rotate around X according to time
const rotateX = MDN.rotateXMatrix(now * 0.0003);
// Rotate around Y according to time slightly faster
const rotateY = MDN.rotateYMatrix(now * 0.0005);
// Move slightly down
const position = MDN.translateMatrix(0, -0.1, 0);
// Multiply together, make sure and read them in opposite order
this.transforms.model = MDN.multiplyArrayOfMatrices([
position, // step 4
rotateY, // step 3
rotateX, // step 2
scale, // step 1
]);
};
Um diese im Shader zu verwenden, muss sie an eine Uniform Location gesetzt werden. Die Positionen für die Uniformen werden im locations-Objekt gespeichert, wie unten gezeigt:
this.locations.model = gl.getUniformLocation(webglProgram, "model");
Und schließlich wird das Uniform auf diese Position gesetzt. Dies übergibt die Matrix an die GPU.
gl.uniformMatrix4fv(
this.locations.model,
false,
new Float32Array(this.transforms.model),
);
Im Shader wird jeder Position-Scheitelpunkt zuerst in eine homogene Koordinate (ein vec4-Objekt) transformiert und dann mit der Modellmatrix multipliziert.
gl_Position = model * vec4(position, 1.0);
Hinweis: In JavaScript erfordert die Matrixmultiplikation eine benutzerdefinierte Funktion, während sie im Shader in die Sprache mit dem einfachen * Operator eingebaut ist.
Die Ergebnisse

An diesem Punkt ist der w-Wert des transformierten Punktes immer noch 1.0. Der Würfel hat immer noch keine Perspektive. Der nächste Abschnitt wird dieses Setup übernehmen und die w-Werte modifizieren, um etwas Perspektive zu bieten.
Übungen
- Verkleinern Sie das Quadrat mit der Skalierungsmatrix und positionieren Sie es an verschiedenen Stellen innerhalb des Clip Space.
- Versuchen Sie, es außerhalb des Clip Space zu bewegen.
- Ändern Sie die Größe des Fensters und beobachten Sie, wie sich das Quadrat verzerrt.
- Fügen Sie eine
rotateZ-Matrix hinzu.
Division durch W
Ein einfacher Weg, um etwas Perspektive auf unser Modell des Würfels zu bekommen, besteht darin, die Z-Koordinate zu nehmen und sie auf die w-Koordinate zu kopieren. Normalerweise wird bei der Umwandlung eines kartesischen Punktes in eine homogene ein (x,y,z,1), aber wir werden es zu etwas wie (x,y,z,z) setzen. In Wirklichkeit wollen wir sicherstellen, dass z für Punkte im Blickfeld größer als 0 ist, daher werden wir es leicht ändern, indem wir den Wert zu ((1.0 + z) * scaleFactor) ändern. Dies wird einen Punkt, der normalerweise im Clip Space liegt (-1 bis 1), in einen Raum bewegen, der eher wie (0 bis 1) ist, abhängig davon, wie der Skalierungsfaktor eingestellt ist. Der Skalierungsfaktor ändert den endgültigen w-Wert insgesamt entweder höher oder niedriger.
Der Shader-Code sieht so aus.
// First transform the point
vec4 transformedPosition = model * vec4(position, 1.0);
// How much effect does the perspective have?
float scaleFactor = 0.5;
// Set w by taking the z value which is typically ranged -1 to 1, then scale
// it to be from 0 to some number, in this case 0-1.
float w = (1.0 + transformedPosition.z) * scaleFactor;
// Save the new gl_Position with the custom w component
gl_Position = vec4(transformedPosition.xyz, w);
Die Ergebnisse
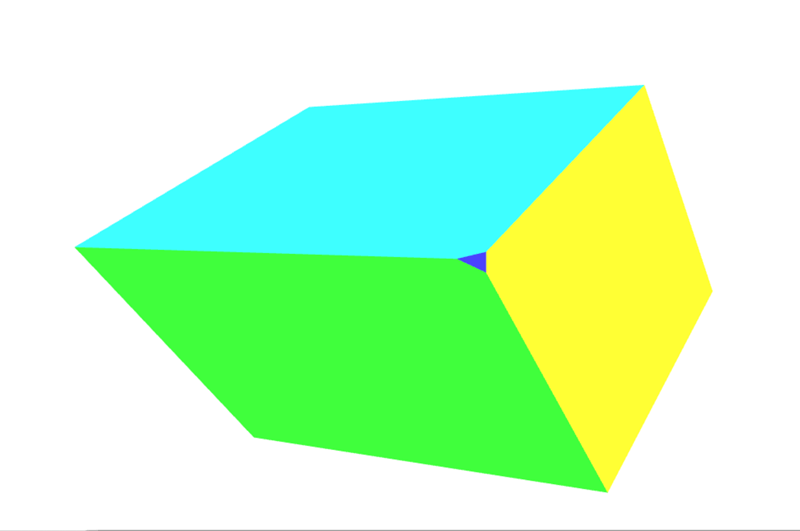
Sehen Sie das kleine dunkelblaue Dreieck? Dies ist eine zusätzliche Fläche, die unserem Objekt hinzugefügt wurde, weil die Drehung unserer Form dazu geführt hat, dass diese Ecke außerhalb des Clip Space ragt, was dazu führt, dass die Ecke abgeschnitten wird. Siehe Perspektivprojektionsmatrix unten für eine Einführung, wie man komplexere Matrizen verwendet, um das Clipping zu kontrollieren und zu verhindern.
Übung
Wenn das ein bisschen abstrakt klingt, öffnen Sie den Vertex-Shader und spielen Sie mit dem Skalierungsfaktor herum und beobachten Sie, wie er die Vertices mehr zur Oberfläche schrumpfen lässt. Ändern Sie die Werte der w-Komponente vollständig für wirklich psychedelische Darstellungen des Raumes.
Im nächsten Abschnitt werden wir diesen Schritt, das Z in den w-Slot zu kopieren, in eine Matrix umwandeln.
Einfaches Projektion
Der letzte Schritt des Auffüllens der w-Komponente kann tatsächlich mit einer einfachen Matrix erreicht werden. Starten Sie mit der Einheitsmatrix:
const identity = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1];
MDN.multiplyPoint(identity, [2, 3, 4, 1]);
//> [2, 3, 4, 1]
Dann verschieben Sie die letzte Spalte um eins nach oben.
const copyZ = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0];
MDN.multiplyPoint(copyZ, [2, 3, 4, 1]);
//> [2, 3, 4, 4]
Im letzten Beispiel führten wir jedoch (z + 1) * scaleFactor aus:
const scaleFactor = 0.5;
const simpleProjection = [
1,
0,
0,
0,
0,
1,
0,
0,
0,
0,
1,
scaleFactor,
0,
0,
0,
scaleFactor,
];
MDN.multiplyPoint(simpleProjection, [2, 3, 4, 1]);
//> [2, 3, 4, 2.5]
Wenn wir es ein wenig weiter aufschlüsseln, können wir sehen, wie das funktioniert:
let x = 2 * 1 + 3 * 0 + 4 * 0 + 1 * 0;
let y = 2 * 0 + 3 * 1 + 4 * 0 + 1 * 0;
let z = 2 * 0 + 3 * 0 + 4 * 1 + 1 * 0;
let w = 2 * 0 + 3 * 0 + 4 * scaleFactor + 1 * scaleFactor;
Die letzte Zeile könnte vereinfacht werden zu:
w = 4 * scaleFactor + 1 * scaleFactor;
Dann, indem der Skalierungsfaktor herausgezogen wird, erhalten wir dies:
w = (4 + 1) * scaleFactor;
Das ist genau das gleiche wie (z + 1) * scaleFactor, das wir im vorherigen Beispiel verwendet haben.
Im Box-Demo wird eine zusätzliche Methode computeSimpleProjectionMatrix() hinzugefügt. Diese wird in der draw()-Methode aufgerufen und der Skalierungsfaktor wird ihr übergeben. Das Ergebnis sollte identisch mit dem letzten Beispiel sein:
CubeDemo.prototype.computeSimpleProjectionMatrix = function (scaleFactor) {
this.transforms.projection = [
1,
0,
0,
0,
0,
1,
0,
0,
0,
0,
1,
scaleFactor,
0,
0,
0,
scaleFactor,
];
};
Das Resultat ist zwar identisch, jedoch ist der entscheidende Schritt hier im Vertex-Shader. Anstatt den Vertex direkt zu modifizieren, wird er mit einer zusätzlichen Projektionsmatrix multipliziert, die (wie der Name schon sagt) 3D-Punkte auf eine 2D-Zeichenfläche projiziert:
// Make sure to read the transformations in reverse order
gl_Position = projection * model * vec4(position, 1.0);
Die Ergebnisse
Der Betrachtungsfrustum
Bevor wir darauf eingehen, wie man eine Perspektivprojektionsmatrix berechnet, müssen wir das Konzept des Betrachtungsfrustums (auch bekannt als Sichtfrustum) einführen. Dies ist der Raumabschnitt, dessen Inhalt dem Benutzer derzeit sichtbar ist. Es ist der 3D-Raumabschnitt, der durch das Sichtfeld und die Distanzen definiert wird, die als nächstgelegener und entferntester Inhalt gerendert werden sollen.
Beim Rendern müssen wir bestimmen, welche Polygone gerendert werden müssen, um die Szene darzustellen. Das ist es, was das Betrachtungsfrustum definiert. Aber was ist überhaupt ein Frustum?
Ein Frustum ist der 3D-Körper, der entsteht, wenn ein beliebiger solider Körper durch zwei parallele Ebenen geschnitten wird. Betrachten Sie unsere Kamera, die einen Bereich betrachtet, der direkt vor ihrer Linse beginnt und sich in die Ferne erstreckt. Der sichtbare Bereich ist eine vierseitige Pyramide, deren Spitze an der Linse, deren vier Seiten den Umfang ihrer peripheren Sichtweite entsprechen, und deren Basis bei der maximal sichtbaren Entfernung der Welt liegt, wie folgt:
Wenn wir dies verwenden würden, um die zu rendernden Polygone in jedem Bild zu bestimmen, müsste unser Renderer alle Polygone innerhalb dieser Pyramide rendern, bis ins Unendliche, einschließlich Polygonen, die sehr nah an der Linse sind - wahrscheinlich zu nah, um nützlich zu sein (und sicherlich Dinge einschließend, die so nah sind, dass ein echter Mensch sie im selben Setting nicht fokussieren könnte).
Der erste Schritt zur Reduzierung der Polygonanzahl, die wir berechnen und rendern müssen, besteht darin, diese Pyramide in das Betrachtungsfrustum zu verwandeln. Die beiden Ebenen, die wir verwenden werden, um Vertices abzuschneiden, um die Polygonanzahl zu verringern, sind die nähere Schnittebene und die weite Schnittebene.
In WebGL werden die nahe und die weit entfernte Schnittebene definiert, indem die Entfernung von der Linse zum nächsten Punkt auf einer Ebene angegeben wird, die senkrecht zur Betrachtungsrichtung steht. Alles, was näher an der Linse liegt als die nahe Schnittebene oder weiter davon entfernt als die weite Schnittebene, wird entfernt. Dies führt zum Betrachtungsfrustum, das folgendermaßen aussieht:
Das anzuzeigende Objektset für jedes Bild wird im Wesentlichen erstellt, indem mit dem Set aller Objekte in der Szene begonnen wird. Danach werden alle Objekte entfernt, die vollständig außerhalb des Betrachtungsfrustums liegen. Anschließend werden Objekte, die teilweise über das Betrachtungsfrustum hinausragen, durch das Entfernen von Polygonen, die vollständig außerhalb des Frustums liegen, und durch das Schneiden der Polygone, die das Frustum überschreiten, so dass sie es nicht mehr verlassen, abgeschnitten.
Sobald dies geschehen ist, haben wir das größte Set von Polygonen, die vollständig innerhalb des Betrachtungsfrustums liegen. Diese Liste wird normalerweise weiter reduziert, indem Prozesse wie Back-Face Culling (das Entfernen von Polygonen, deren Rückseite zur Kamera zeigt) und Okklusions-Culling mittels versteckter Flächenermittlung (das Entfernen von Polygonen, die nicht gesehen werden können, weil sie vollständig von Polygonen verdeckt werden, die näher an der Linse sind) verwendet.
Perspektivprojektionsmatrix
Bis zu diesem Punkt haben wir unser eigenes 3D-Rendering-Setup Schritt für Schritt aufgebaut. Unser derzeitiger Code, wie wir ihn aufgebaut haben, weist jedoch einige Probleme auf. Zum einen wird er verzerrt, wann immer man unsere Fenstergröße ändert. Ein weiteres ist, dass unsere einfache Projektion nicht mit einer breiten Palette von Werten für die Szenendaten umgeht. Die meisten Szenen funktionieren nicht im Clip Space. Es wäre hilfreich, die relevante Entfernung zur Szene zu definieren, damit die Präzision nicht beim Umwandeln der Zahlen verloren geht. Schließlich ist es sehr hilfreich, eine feine Kontrolle darüber zu haben, welche Punkte innerhalb und außerhalb des Clip Space platziert werden. In den vorhergehenden Beispielen werden die Ecken des Würfels gelegentlich abgeschnitten.
Die Perspektivprojektionsmatrix ist eine Art Projektionsmatrix, die all diese Anforderungen erfüllt. Die Mathematik wird auch ein wenig komplexer und wird in diesen Beispielen nicht vollständig erklärt. Kurz gesagt, es kombiniert die Division durch w (wie in den vorherigen Beispielen gemacht) mit einigen genialen Manipulationen basierend auf ähnlichen Dreiecken. Wenn Sie eine vollständige Erklärung der Mathematik dahinter lesen möchten, schauen Sie sich einige der folgenden Links an:
- OpenGL-Projektionsmatrix
- Perspektivprojektion
- Versuche das Math hinter der Perspektivmatrix in WebGL zu verstehen
Ein wichtiger Punkt, den Sie über die Perspektivprojektionsmatrix unten beachten sollten, ist, dass sie die z-Achse umkehrt. Im Clip Space zeigt die z+-Achse vom Betrachter weg, während sie mit dieser Matrix zum Betrachter kommt.
Der Grund, die z-Achse zu flippen, besteht darin, dass das Clip Space-Koordinatensystem ein linkshändiges Koordinatensystem ist (wobei die z-Achse vom Betrachter weg und in den Bildschirm hineinzeigt), während die Konvention in Mathematik, Physik und 3D-Modellierung sowie im Ansicht-/Augenkoordinatensystem in OpenGL darin besteht, ein rechtshändiges Koordinatensystem zu verwenden (z-Achse zeigt aus dem Bildschirm auf den Betrachter zu). Mehr dazu in den relevanten Wikipedia-Artikeln: Kartesisches Koordinatensystem, Rechte-Hand-Regel.
Lassen Sie uns einen Blick auf eine perspectiveMatrix()-Funktion werfen, die die Perspektivprojektionsmatrix berechnet.
MDN.perspectiveMatrix = function (
fieldOfViewInRadians,
aspectRatio,
near,
far,
) {
const f = 1.0 / Math.tan(fieldOfViewInRadians / 2);
const rangeInv = 1 / (near - far);
return [
f / aspectRatio,
0,
0,
0,
0,
f,
0,
0,
0,
0,
(near + far) * rangeInv,
-1,
0,
0,
near * far * rangeInv * 2,
0,
];
};
Die vier Parameter dieser Funktion sind:
fieldOfViewInRadians-
Ein Winkel in Radiant, der angibt, wie viel der Szene dem Betrachter gleichzeitig sichtbar ist. Je größer die Zahl ist, desto mehr ist sichtbar durch die Kamera. Die Geometrie an den Rändern wird immer mehr verzerrt, was einer Weitwinkeloptik entspricht. Wenn das Sichtfeld größer ist, werden die Objekte typischerweise kleiner. Wenn das Sichtfeld kleiner ist, dann kann die Kamera immer weniger in der Szene sehen. Die Objekte werden viel weniger durch die Perspektive verzerrt und Objekte scheinen viel näher an der Kamera.
aspectRatio-
Das Seitenverhältnis der Szene, das ihrer Breite geteilt durch ihre Höhe entspricht. In diesen Beispielen ist das die Fensterbreite geteilt durch die Fensterhöhe. Die Einführung dieses Parameters löst endlich das Problem, bei dem das Modell verzerrt wird, wenn die Leinwand in der Größe verändert und umgestaltet wird.
nearClippingPlaneDistance-
Eine positive Zahl, die die Distanz in den Bildschirm zu einer Ebene angibt, die senkrecht zum Boden steht, näher an der alles abgeschnitten wird. Dies wird im Clip Space auf -1 abgebildet und sollte nicht auf 0 gesetzt werden.
farClippingPlaneDistance-
Eine positive Zahl, die die Entfernung zur Ebene angibt, jenseits der Geometrie abgeschnitten wird. Dies wird im Clip Space auf 1 abgebildet. Dieser Wert sollte vernünftigerweise nahe an der Entfernung der Geometrie gehalten werden, um Genauigkeitsfehler zu vermeiden, die sich während des Renderns einschleichen.
In der neuesten Version des Box-Demos wurde die computeSimpleProjectionMatrix()-Methode durch die computePerspectiveMatrix()-Methode ersetzt.
CubeDemo.prototype.computePerspectiveMatrix = function () {
const fieldOfViewInRadians = Math.PI * 0.5;
const aspectRatio = window.innerWidth / window.innerHeight;
const nearClippingPlaneDistance = 1;
const farClippingPlaneDistance = 50;
this.transforms.projection = MDN.perspectiveMatrix(
fieldOfViewInRadians,
aspectRatio,
nearClippingPlaneDistance,
farClippingPlaneDistance,
);
};
Der Shader-Code ist identisch mit dem vorherigen Beispiel:
gl_Position = projection * model * vec4(position, 1.0);
Zusätzlich (nicht angezeigt) wurden die Positions- und Skalierungsmatrizen des Modells geändert, um ihn aus dem Clip Space in das größere Koordinatensystem zu bringen.
Die Ergebnisse
Übungen
- Experimentieren Sie mit den Parametern der Perspektivprojektionsmatrix und der Modellmatrix.
- Ersetzen Sie die Perspektivprojektionsmatrix durch die orthografische Projektion. In dem MDN WebGL Shared Code finden Sie die
MDN.orthographicMatrix(). Diese kann dieMDN.perspectiveMatrix()-Funktion inCubeDemo.prototype.computePerspectiveMatrix()ersetzen.
Betrachtungsmatrix
Während einige Grafikbibliotheken eine virtuelle Kamera haben, die positioniert und ausgerichtet werden kann, während eine Szene erstellt wird, haben OpenGL (und damit auch WebGL) dies nicht. Hier kommt die Betrachtungsmatrix ins Spiel. Ihre Aufgabe ist es, die Objekte der Szene zu übersetzen, zu rotieren und zu skalieren, um sie relativ zum Betrachter korrekt zu platzieren, basierend auf der Position und Orientierung des Betrachters.
Eine Kamera simulieren
Dies nutzt einen der grundlegenden Aspekte von Einsteins spezieller Relativitätstheorie: das Prinzip der Bezugssysteme und der relativen Bewegung besagt, dass man aus der Perspektive des Betrachters das Ändern der Position und Ausrichtung des Betrachters durch das Aufbringen der gegenteiligen Änderung auf die Objekte in der Szene simulieren kann. Entweder der Weg, das Ergebnis erscheint dem Betrachter als identisch.
Stellen Sie sich eine Kiste vor, die auf einem Tisch sitzt, und eine Kamera, die auf dem Tisch einen Meter entfernt steht, auf die Kiste zeigt, wobei die Vorderseite zur Kamera zeigt. Betrachten Sie nun das Entfernen der Kamera von der Kiste, bis sie zwei Meter entfernt ist (durch Hinzufügen eines Meters zur Z-Position der Kamera) und sie dann 10 Zentimeter nach links schieben. Die Box entfernt sich von der Kamera um diesen Betrag und gleitet leicht nach rechts, wodurch sie der Kamera kleiner erscheint und eine kleine Menge ihrer linken Seite exponiert.
Setzen wir nun die Szene zurück, platzieren die Kiste wieder an ihrem Ausgangspunkt, mit der Kamera zwei Meter von der Kiste entfernt und direkt auf die Kiste gerichtet. Dieses Mal jedoch ist die Kamera auf dem Tisch fixiert und kann nicht bewegt oder gedreht werden. Das ist das Arbeiten in WebGL. Wie simulieren wir dann das Bewegen der Kamera durch den Raum?
Anstatt die Kamera rückwärts und nach links zu bewegen, wenden wir die inverse Transformation auf die Box an: Wir bewegen die Box rückwärts einen Meter und dann 10 Zentimeter nach rechts. Das Ergebnis ist aus der Perspektive jedes der beiden Objekte identisch.
Der letzte Schritt in all dem ist die Erstellung der Betrachtungsmatrix, die die Objekte in der Szene transformiert, so dass sie positioniert sind, um die aktuelle Position und Orientierung der Kamera zu simulieren. Unser Code, wie er jetzt steht, kann den Würfel im Weltall bewegen und alles perspektivisch projizieren, aber wir können die Kamera noch nicht bewegen.
Stellen Sie sich das Drehen eines Films mit einer physischen Kamera vor. Sie haben die Freiheit, die Kamera im Wesentlichen überall zu platzieren, wo Sie möchten, und die Kamera in jede beliebige Richtung auszurichten. Um dies in 3D-Grafiken zu simulieren, verwenden wir eine Betrachtungsmatrix, um die Position und Drehung der physischen Kamera zu simulieren.
Im Gegensatz zur Modellmatrix, die die Modelle direkt transformiert, bewegt die Betrachtungsmatrix eine abstrakte Kamera. In Wirklichkeit bewegt der Vertex-Shader immer noch nur die Modelle, während die "Kamera" an Ort und Stelle bleibt. Damit das korrekt funktioniert, muss die inverse Transformationsmatrix verwendet werden. Die inverse Matrix kehrt im Wesentlichen eine Transformation um, so dass, wenn wir die Kamerasicht nach vorne bewegen, die inverse Matrix die Objekte in der Szene nach hinten bewegt.
Die folgende Methode computeViewMatrix() animiert die Betrachtungsmatrix, indem sie ein- und ausgefahren und nach links und rechts bewegt wird.
CubeDemo.prototype.computeViewMatrix = function (now) {
const moveInAndOut = 20 * Math.sin(now * 0.002);
const moveLeftAndRight = 15 * Math.sin(now * 0.0017);
// Move the camera around
const position = MDN.translateMatrix(moveLeftAndRight, 0, 50 + moveInAndOut);
// Multiply together, make sure and read them in opposite order
const matrix = MDN.multiplyArrayOfMatrices([
// Exercise: rotate the camera view
position,
]);
// Inverse the operation for camera movements, because we are actually
// moving the geometry in the scene, not the camera itself.
this.transforms.view = MDN.invertMatrix(matrix);
};
Der Shader verwendet nun drei Matrizen.
gl_Position = projection * view * model * vec4(position, 1.0);
Nach diesem Schritt schneidet die GPU-Pipeline die Punkte außerhalb des Bereichs und sendet das Modell zum Fragment-Shader für die Rasterung.
Die Ergebnisse
Beziehung der Koordinatensysteme
An diesem Punkt wäre es vorteilhaft, einen Schritt zurückzutreten und sich die verschiedenen Koordinatensysteme anzusehen und zu beschriften, die wir verwenden. Zuerst werden die Vertices des Würfels in Modellraum definiert. Um das Modell in der Szene zu bewegen. Diese Vertices müssen in Weltraum umgewandelt werden, indem die Modellmatrix angewendet wird.
Modellraum → Modellmatrix → Weltraum
Die Kamera hat noch nichts getan, und die Punkte müssen erneut bewegt werden. Derzeit befinden sie sich im Weltraum, aber sie müssen in Sichtraum gebracht werden (mithilfe der Betrachtungsmatrix), um die Positionierung der Kamera darzustellen.
Weltraum → Betrachtungsmatrix → Sichtraum
Schließlich muss eine Projektion (in unserem Fall die Perspektivprojektionsmatrix) hinzugefügt werden, um die Weltkoordinaten in Clip Space-Koordinaten zu überführen.
Sichtraum → Projektionsmatrix → Clip Space
Übung
- Bewegen Sie die Kamera durch die Szene.
- Fügen Sie einige Rotationsmatrizen zur Betrachtungsmatrix hinzu, um die Ansicht zu verändern.
- Verfolgen Sie schließlich die Position der Maus. Verwenden Sie zwei Rotationsmatrizen, um die Kamera in Abhängigkeit von der Position der Maus im Bildschirm nach oben und unten schauen zu lassen.