MathML-Textcontainer
Jetzt, da Sie eine bessere Vorstellung von MathML haben, konzentrieren wir uns auf Textcontainer (Variablen, Zahlen, Operatoren usw.), die als Bausteine von MathML-Formeln dienen.
Unicode-Zeichen für Mathematik
Mathematische Formeln beinhalten viele besondere Zeichen, zum Beispiel griechische Buchstaben (z. B. Δ), Fraktur-Buchstaben (z. B. 𝔄), durchgestrichene Buchstaben (z. B. ℂ), Binäroperationen (z. B. ≠), Pfeile (z. B. ⇒), Integralzeichen (z. B. ∮), Summenzeichen (z. B. ∑), logische Symbole (z. B. ∀), Klammern (z. B. ⌊) und viele mehr. Der Wikipedia-Artikel Mathematical operators and symbols in Unicode bietet einen guten Überblick über die verwendeten Zeichen.
Da die meisten dieser Zeichen nicht Teil des Basic Latin Unicode-Blocks sind, wird empfohlen, die Zeichenkodierung Ihres Dokuments festzulegen und es mit geeigneten Webfonts auszuliefern. Hier ist eine grundlegende Vorlage, um UTF-8-Codierung und die Latin Modern Math Schriftart zu verwenden:
<!doctype html>
<html lang="en-US">
<head>
<meta charset="utf-8" />
<title>My page with math characters</title>
<link
rel="stylesheet"
href="https://fred-wang.github.io/MathFonts/LatinModern/mathfonts.css" />
</head>
<body>
<p style="font-family: Latin Modern Math">∀A∊𝔰𝔩(n,𝔽),TrA=0</p>
</body>
</html>
Ein wenig Semantik
Wir haben im Artikel Erste Schritte mit MathML festgestellt, dass der Text in MathML-Formeln in spezifischen Containerelementen wie <mn> oder <mo> eingebettet ist. Allgemeiner muss jeder Text in MathML-Formeln in solchen Containerelementen enthalten sein, die als Token-Elemente bezeichnet werden. Darüber hinaus bietet MathML mehrere Token-Elemente, um unterschiedliche Bedeutungen des Textinhalts zu unterscheiden:
- Das
<mi>-Element, das einen "Bezeichner" darstellt, der ein symbolischer Name oder beliebiger Text sein könnte. Beispiele:<mi>x</mi>(Variable),<mi>cos</mi>(Funktionsname) und<mi>π</mi>(symbolische Konstante). - Das
<mn>-Element repräsentiert ein "numerisches Literal" oder andere Daten, die als numerisches Literal dargestellt werden sollen. Beispiele:<mn>2</mn>(Ganzzahl),<mn>0.123</mn>(Dezimalzahl) oder<mn>0xFFEF</mn>(hexadezimaler Wert). - Das
<mo>-Element repräsentiert einen Operator oder alles, was als Operator dargestellt werden soll. Zum Beispiel<mo>+</mo>(binäre Operation),<mo>≤</mo>(binäre Relation),<mo>∑</mo>(Summenzeichen) oder<mo>[</mo>(Klammer). - Das
<mtext>-Element wird verwendet, um beliebigen Text darzustellen. Zum Beispiel kurze Wörter in Formeln wie<mtext>wenn<mtext>oder<mtext>abbildet auf</mtext>.
Aktives Lernen: Token-Elemente erkennen
Unten ist ein komplexeres Beispiel, das besagt, dass der Absolutwert einer reellen Zahl gleich dieser Zahl ist, wenn und nur wenn sie nicht negativ ist. Finden Sie die verschiedenen Token-Elemente und wofür sie verwendet werden. Jedes Mal, wenn Sie den entsprechenden Text anklicken, wird er hervorgehoben und eine Bestätigungsnachricht angezeigt.
Schließlich lesen Sie den MathML-Quellcode, um zu prüfen, ob er Ihren Erwartungen entspricht:
<math display="block">
<mrow>
<mrow>
<mo>|</mo>
<mi>x</mi>
<mo>|</mo>
</mrow>
<mo>=</mo>
<mi>x</mi>
</mrow>
<mtext> iff </mtext>
<mrow>
<mi>x</mi>
<mo>≥</mo>
<mn>0</mn>
</mrow>
</math>
Hinweis:
Es ist manchmal schwierig zu entscheiden, welches Token-Element für einen bestimmten Textinhalt zu verwenden ist. In der Praxis sollte die Wahl des falschen Elements keine großen Probleme verursachen, da alle Token-Elemente von Browser-Implementierungen im Allgemeinen gleich gerendert werden (für die visuelle Darstellung und für Assistenztechnologien). Dennoch haben die <mi>- und <mo>-Elemente spezielle Unterscheidungsmerkmale, die man beachten sollte. Diese werden in den folgenden Abschnitten erklärt.
Automatische Kursivsetzung von <mi>
Eine typografische Konvention in der Mathematik ist die Verwendung von kursiven Buchstaben für Variablen. Um dies zu unterstützen, können <mi>-Elemente mit einem einzigen Zeichen automatisch kursiv dargestellt werden. Dies gilt für alle Buchstaben aus dem lateinischen und griechischen Alphabet. Vergleichen Sie die Darstellung der beiden <mi>-Elemente in der folgenden Formel:
<math>
<mi>sin</mi>
<mi>x</mi>
</math>
Hinweis: Diese Tabelle aus MathML Core bietet die vollständige Liste der Zeichen, die der Kursivierung unterliegen, zusammen mit den entsprechenden kursiven Zeichen.
Rückgängigmachen der automatischen Kursivsetzung von <mi>
Um diese standardmäßige Kursivtransformation rückgängig zu machen, können Sie ein mathvariant="normal"-Attribut an das <mi>-Element anhängen.
Vergleichen Sie die Darstellung der Großbuchstaben Gamma in der folgenden Formel:
<math>
<mi>Γ</mi>
<mi mathvariant="normal">Γ</mi>
</math>
Hinweis: Obwohl Sie diese Transformation anwenden können, würden Sie normalerweise einfach die gewünschten Mathematischen Alfanumerischen Symbole verwenden.
Operator-Eigenschaften von <mo>
MathML enthält ein Operator-Wörterbuch, das die Standardeigenschaften von <mo>-Elementen je nach Inhalt und Position innerhalb seines Containers (Präfix, Infix oder Postfix) definiert. Betrachten wir ein konkretes Beispiel:
<table>
<tr>
<td>Prefix plus</td>
<td>
<math>
<mo>+</mo>
<mi>i</mi>
</math>
</td>
</tr>
<tr>
<td>Infix plus</td>
<td>
<math>
<mi>j</mi>
<mo>+</mo>
<mi>i</mi>
</math>
</td>
</tr>
<tr>
<td>Prefix sum</td>
<td>
<math>
<mo>∑</mo>
<mi>i</mi>
</math>
</td>
</tr>
</table>
Dieses Beispiel sollte ähnlich dem Screenshot unten dargestellt werden. Beachten Sie den Abstand zwischen den <mi>i</mi>-Elementen und dem vorangehenden <mo>: kein Abstand für das Präfix-Plus, etwas Abstand für das Infix-Plus und ein kleinerer Abstand für das Präfix-Summenzeichen.
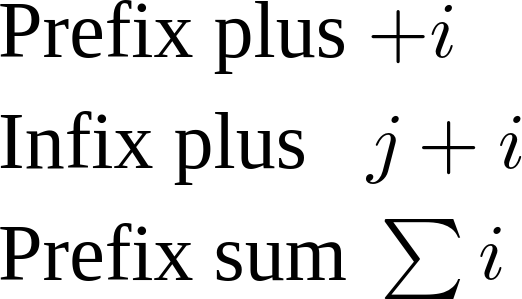
Operatoren haben viele andere Eigenschaften, die wir später noch ausführlicher sehen werden. Merken Sie sich vorerst, ein <mo>-Container für Zeichen im Operator-Wörterbuch zu verwenden und Unterausdrücke richtig mit <mrow>-Elementen zu gruppieren, um MathML-Renderer zu unterstützen.
Aktives Lernen: den Unterschied erkennen
Jetzt, da Sie ein wenig mit den besonderen Merkmalen von <mi> und <mo> vertraut sind, lassen Sie uns das <p>-Element im Beispiel oben auf der Seite mit etwas tatsächlichem MathML umschreiben. Vergleichen Sie die visuelle Darstellung in Ihrem Browser und erklären Sie die Unterschiede zur reinen Textversion.
<!doctype html>
<html lang="en-US">
<head>
<meta charset="utf-8" />
<title>My page with math characters</title>
<link
rel="stylesheet"
href="https://fred-wang.github.io/MathFonts/LatinModern/mathfonts.css" />
</head>
<body>
<p style="font-family: Latin Modern Math">∀A∊𝔰𝔩(n,𝔽),TrA=0</p>
<p>
<math>
<mo>∀</mo>
<mrow>
<mi>A</mi>
<mo>∊</mo>
<mrow>
<mi>𝔰𝔩</mi>
<mrow>
<mo>(</mo>
<mi>n</mi>
<mo>,</mo>
<mi>𝔽</mi>
<mo>)</mo>
</mrow>
</mrow>
</mrow>
<mo>,</mo>
<mrow>
<mrow>
<mi>Tr</mi>
<mi>A</mi>
</mrow>
<mo>=</mo>
<mn>0</mn>
</mrow>
</math>
</p>
<input id="showSolution" type="button" value="Show solution" />
<div id="solution"></div>
</body>
</html>
Hinweis: Ein offensichtlicher Unterschied ist, dass der Quellcode mit MathML viel ausführlicher wurde. Denken Sie daran, dass dieses Tutorial dazu dient, die Sprache zu erlernen, aber in der Praxis wird MathML-Inhalt in der Regel nicht manuell geschrieben. Weitere Informationen finden Sie auf der Seite MathML erstellen.
Aktives Lernen: dehnbare Operatoren
Das Operator-Wörterbuch definiert eine Standardeigenschaft stretchy sowie die entsprechende stretch axis für einige Operatoren. Ein Operator kann beispielsweise standardmäßig vertikal gestreckt werden, um die maximale Höhe der nicht dehnbaren Geschwister innerhalb seines <mrow>-Containers abzudecken. Indem man die vorherige Übung ein wenig anpasst, kann man Operatoren vertikal dehnen. Können Sie sie finden?
Wie üblich sind Sie eingeladen, den Quellcode zu lesen, wenn Sie fertig sind:
<math display="block">
<mrow>
<mrow>
<mo>|</mo>
<mfrac>
<mn>1</mn>
<mi>x</mi>
</mfrac>
<mo>|</mo>
</mrow>
<mo>=</mo>
<mfrac>
<mn>1</mn>
<mrow>
<mo>|</mo>
<mi>x</mi>
<mo>|</mo>
</mrow>
</mfrac>
<mo>=</mo>
<mfrac>
<mn>1</mn>
<mi>x</mi>
</mfrac>
</mrow>
<mtext> iff </mtext>
<mrow>
<mi>x</mi>
<mo>≥</mo>
<mn>0</mn>
</mrow>
</math>
Warnung: Besondere Mathe-Schriftarten sind allgemein erforderlich, um dieses Dehnen zu ermöglichen, das vorherige Beispiel stützt sich auf Webfonts.
Zusammenfassung
In diesem Artikel haben wir einige Token-Elemente kennengelernt, die als Textcontainer sowie ihre unterschiedlichen Semantiken dienen, nämlich <mi> (Bezeichner), <mn> (Zahlen), <mo> (Operatoren), <mtext> (generischer Text). Wir haben spezielle Unicode-Zeichen gesehen, die häufig in mathematischen Formeln vorkommen, und einen Überblick über einige beobachtbare Verhaltensweisen der <mi>- und <mo>-Elemente gegeben. Im nächsten Artikel werden wir sehen, wie man sich auf Token-Elemente stützt, um viel komplexere Ausdrücke wie Brüche und Wurzeln zu erstellen.