MathML-Brüche und -Wurzeln

Aufbauend auf Textcontainern beschreibt dieser Artikel, wie komplexere MathML-Ausdrücke durch das Verschachteln von Brüchen und Wurzeln erstellt werden.

Voraussetzungen:	Grundlegende Software installiert, Grundkenntnisse im Umgang mit Dateien und HTML-Grundlagen (studieren Sie Einführung in HTML).
Ziel:	Vertrautheit mit MathML-Elementen erlangen, die zum Schreiben von Brüchen und Quadratwurzeln verwendet werden.

Teilbäume von `<mfrac>`, `<msqrt>` und `<mroot>`

Im Artikel Einstieg in MathML haben wir bereits das <mfrac>-Element kennengelernt, das zur Beschreibung eines Bruchs verwendet wird. Betrachten wir ein einfaches Beispiel, das neue Elemente für Wurzeln (<msqrt> und <mroot>) hinzufügt:

html

<math>
  <mfrac>
    <mtext>child1</mtext>
    <mtext>child2</mtext>
  </mfrac>
</math>
<br />
<math>
  <msqrt>
    <mtext>child1</mtext>
    <mtext>child2</mtext>
    <mtext>...</mtext>
    <mtext>childN</mtext>
  </msqrt>
</math>
<br />
<math>
  <mroot>
    <mtext>child1</mtext>
    <mtext>child2</mtext>
  </mroot>
</math>

Unten sehen Sie einen Screenshot, wie er von einem Browser gerendert wird:

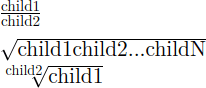
$Screenshot von mfrac, msqrt, mroot$

Wir wissen bereits, dass das <mfrac>-Element als Bruch dargestellt wird: Das erste Kind (der Zähler) wird oberhalb des zweiten Kindes (des Nenners) gezeichnet und durch einen horizontalen Balken getrennt.
Das <msqrt>-Element wird als Quadratwurzel gerendert: Seine Kinder werden wie ein <mrow> angeordnet, dem ein Wurzelsymbol √ vorangestellt ist und das vollständig von einer Überlinie bedeckt wird.
Schließlich wird das <mroot>-Element als n-te Wurzel gerendert: Das erste Element wird vom Radikalsymbol bedeckt, während das zweite Element als Grad der Wurzel dient und als Präfix-Superscript dargestellt wird.

Aktives Lernen: Verschachteln verschiedener Elemente

Hier ist eine Übung, um zu überprüfen, ob Sie die Beziehung zwischen einem MathML-Teilbaum und seiner visuellen Darstellung verstanden haben. Das Dokument enthält eine MathML-Formel und Sie müssen alle Teilbäume überprüfen, die einem Teilbaum in dieser MathML-Formel entsprechen. Sobald Sie fertig sind, können Sie den Quellcode der MathML-Formel inspizieren und überprüfen, ob er Ihren Erwartungen entspricht.

<!doctype html>
<html lang="en-US">
  <head>
    <meta charset="utf-8" />
    <title>My page with math characters</title>
    <link
      rel="stylesheet"
      href="https://fred-wang.github.io/MathFonts/LatinModern/mathfonts.css" />
  </head>
  <body>
    <p>
      <math>
        <mfrac id="mfrac1">
          <msqrt id="msqrt1">
            <mn>2</mn>
          </msqrt>
          <mroot id="mroot1">
            <mn>4</mn>
            <mn>3</mn>
          </mroot>
        </mfrac>
        <mo>+</mo>
        <mroot id="mroot2">
          <mn>5</mn>
          <mfrac id="mfrac2">
            <mn>6</mn>
            <mn>7</mn>
          </mfrac>
        </mroot>
        <mo>+</mo>
        <msqrt id="msqrt2">
          <mn>8</mn>
          <mo>−</mo>
          <mn>9</mn>
        </msqrt>
      </math>
    </p>

    <ol id="options">
      <li>
        <input
          type="checkbox"
          data-comment="Verify the order of children in an mfrac!" />
        An mfrac with an mroot as its first child and an msqrt as its second
        child.
      </li>
      <li>
        <input
          type="checkbox"
          data-highlight="mroot2"
          data-comment="The '6 over 7'-th root of five." />
        An mroot with an mn as its first child and mfrac as its second child.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="This formula does not contain any fraction inside a square root!" />
        An msqrt containing an mfrac element.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="The square root of two."
          data-highlight="msqrt1" />
        An msqrt with one mn child.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="Verify the order of children in an mroot!" />
        An mroot with an mfrac as its first child and mn as its second child.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="The square root of 'eight minus nine'."
          data-highlight="msqrt2" />
        An msqrt with the following list of children: mn, mo, mn.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="The square root of two over the cubic root of four."
          data-highlight="mfrac1" />
        An mfrac with an msqrt as its first child and an mroot as its second
        child.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="mfrac must have exactly two children!" />
        An mfrac with the following list of children: msqrt, mn, msqrt.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="mroot must have exactly two children!" />
        An mroot with one mn child.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="The fraction six over seven."
          data-highlight="mfrac2" />
        An mfrac with two mn children.
      </li>
      <li>
        <input
          type="checkbox"
          data-comment="This formula does not contain any square root with more than two numbers!" />
        An msqrt with five mn children.
      </li>
      <li>
        <input
          type="checkbox"
          data-highlight="mroot1"
          data-comment="The cubic root of four." />
        An mroot with two mn children.
      </li>
    </ol>
    <p>
      <strong id="comment"></strong>
    </p>
    <p>
      <strong id="status"></strong>
    </p>
  </body>
</html>

math {
  font-family:
    Latin Modern Math,
    STIX Two Math;
  font-size: 200%;
}
math .highlight {
  background: pink;
}
math [id] .highlight {
  background: lightblue;
}
p {
  padding: 0.5em;
}

const options = document.getElementById("options");
const comment = document.getElementById("comment");
const checkboxes = Array.from(options.getElementsByTagName("input"));
const status = document.getElementById("status");
function verifyOption(checkbox) {
  let mathml = checkbox.dataset.highlight;
  if (mathml) {
    mathml = document.getElementById(mathml);
  }
  if (checkbox.checked) {
    comment.textContent = checkbox.dataset.comment;
    if (mathml) {
      mathml.classList.add("highlight");
    } else {
      checkbox.checked = false;
    }
  } else {
    comment.textContent = "";
    if (mathml) {
      mathml.classList.remove("highlight");
    }
  }
  const finished = checkboxes.every(
    (checkbox) => !!checkbox.checked === !!checkbox.dataset.highlight,
  );
  status.textContent = finished
    ? "Congratulations, you checked all the correct answers!"
    : "";
}
checkboxes.forEach((checkbox) => {
  checkbox.addEventListener("change", () => {
    verifyOption(checkbox);
  });
});

Dehnbare Radikalsymbole

Wie zuvor gesehen, erstreckt sich die Überlinie der <msqrt>- und <mroot>-Elemente horizontal, um deren Inhalt abzudecken. Tatsächlich dehnt sich aber auch das Wurzelsymbol √, um so hoch wie der Inhalt zu sein.

<link
  rel="stylesheet"
  href="https://fred-wang.github.io/MathFonts/LatinModern/mathfonts.css" />

html

<math display="block">
  <mroot>
    <msqrt>
      <mfrac>
        <mn>1</mn>
        <mn>2</mn>
      </mfrac>
    </msqrt>
    <mn>3</mn>
  </mroot>
</math>

Warnung: Spezielle Mathematik-Schriften werden im Allgemeinen benötigt, um diese Streckung zu ermöglichen, das vorherige Beispiel basiert auf Webschriften.

Brüche ohne Balken

Einige mathematische Konzepte werden manchmal mit bruchähnlichen Notationen wie Binomialkoeffizienten oder Legendre-Symbolen geschrieben. Es ist angemessen, ein <mfrac>-Element zu verwenden, um solche Notationen zu markieren. Für bruchähnliche Notationen, die keinen horizontalen Balken zeichnen, fügen Sie dem <mfrac>-Element ein linethickness="0"-Attribut hinzu:

<link
  rel="stylesheet"
  href="https://fred-wang.github.io/MathFonts/LatinModern/mathfonts.css" />

html

<math display="block">
  <mrow>
    <mo>(</mo>
    <mfrac linethickness="0">
      <mn>3</mn>
      <mn>2</mn>
    </mfrac>
    <mo>)</mo>
  </mrow>
  <mo>=</mo>
  <mn>3</mn>
  <mo>≠</mo>
  <mfrac>
    <mn>3</mn>
    <mn>2</mn>
  </mfrac>
</math>

Hinweis: Obwohl das linethickness-Attribut verwendet werden kann, um eine beliebige Dicke anzugeben, ist es besser, den Standardwert beizubehalten, der aus Parametern berechnet wird, die in der Mathematischen Schrift angegeben sind.

Zusammenfassung

In dieser Lektion haben wir gesehen, wie Brüche und Wurzeln mit den <mfrac>, <msqrt> und <mroot>-Elementen aufgebaut werden. Wir haben einige spezielle Merkmale dieser Elemente bemerkt, nämlich das Bruch- und Radikalsymbol. Wir haben gesehen, wie man das linethickness-Attribut verwendet, um Brüche ohne Balken zu zeichnen. Im nächsten Artikel werden wir mit grundlegenden mathematischen Notationen fortfahren und Indizes betrachten.

Teilbäume von <mfrac>, <msqrt> und <mroot>

Aktives Lernen: Verschachteln verschiedener Elemente

Dehnbare Radikalsymbole

Brüche ohne Balken

Zusammenfassung

Siehe auch

Teilbäume von `<mfrac>`, `<msqrt>` und `<mroot>`